Java模拟并发场景
多线程环境下,我们要如何测试自己写的业务代码是否是线程安全的?
可以用到 CountDownLatch 这个类,让所有线程都 await, 然后 countDown 以后,所有线程共同执行。
1 | package gy.finolo.concurrent; |
多线程环境下,我们要如何测试自己写的业务代码是否是线程安全的?
可以用到 CountDownLatch 这个类,让所有线程都 await, 然后 countDown 以后,所有线程共同执行。
1 | package gy.finolo.concurrent; |
使用安卓搜狗输入法小米版时,经常会误点到如图所示的广告。
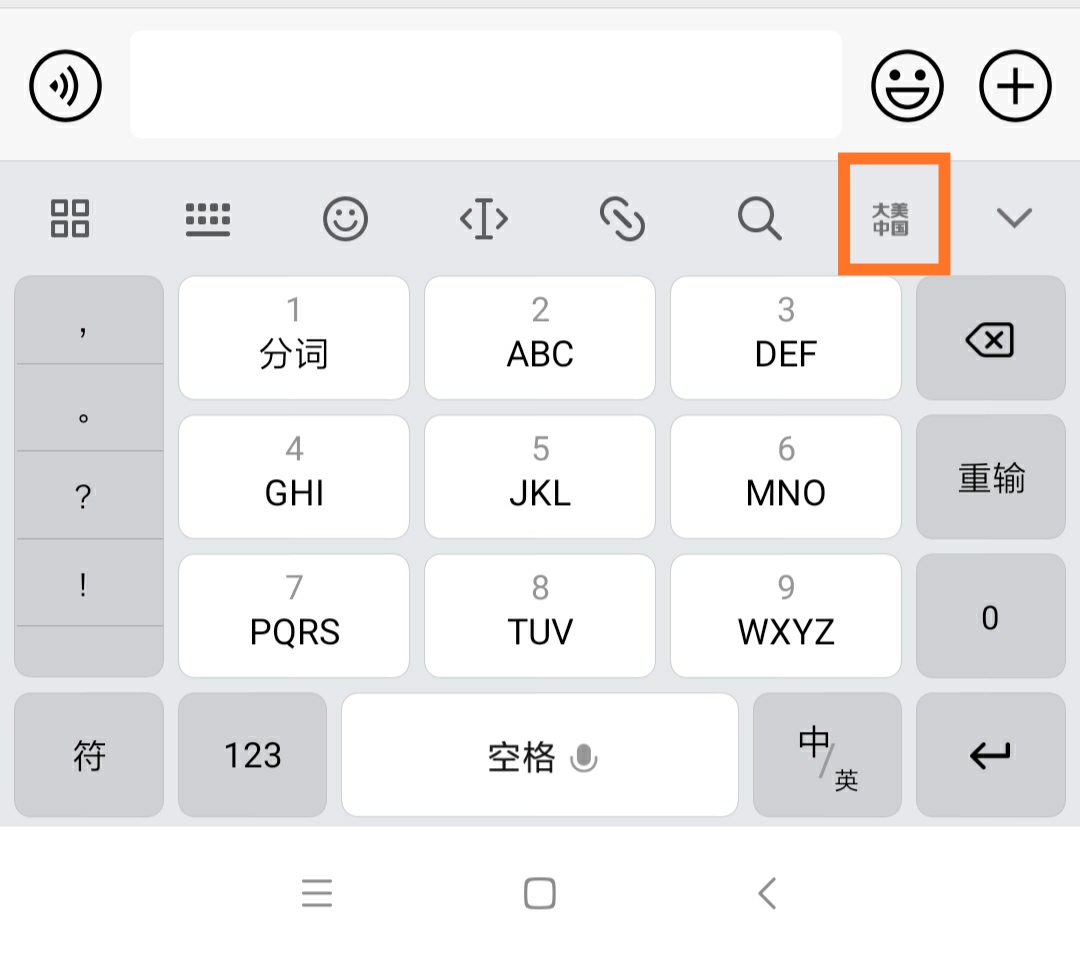
一般会启动小米的一个应用。关掉应用再回到原来页面,要耗费好几秒钟时间,非常恶心。
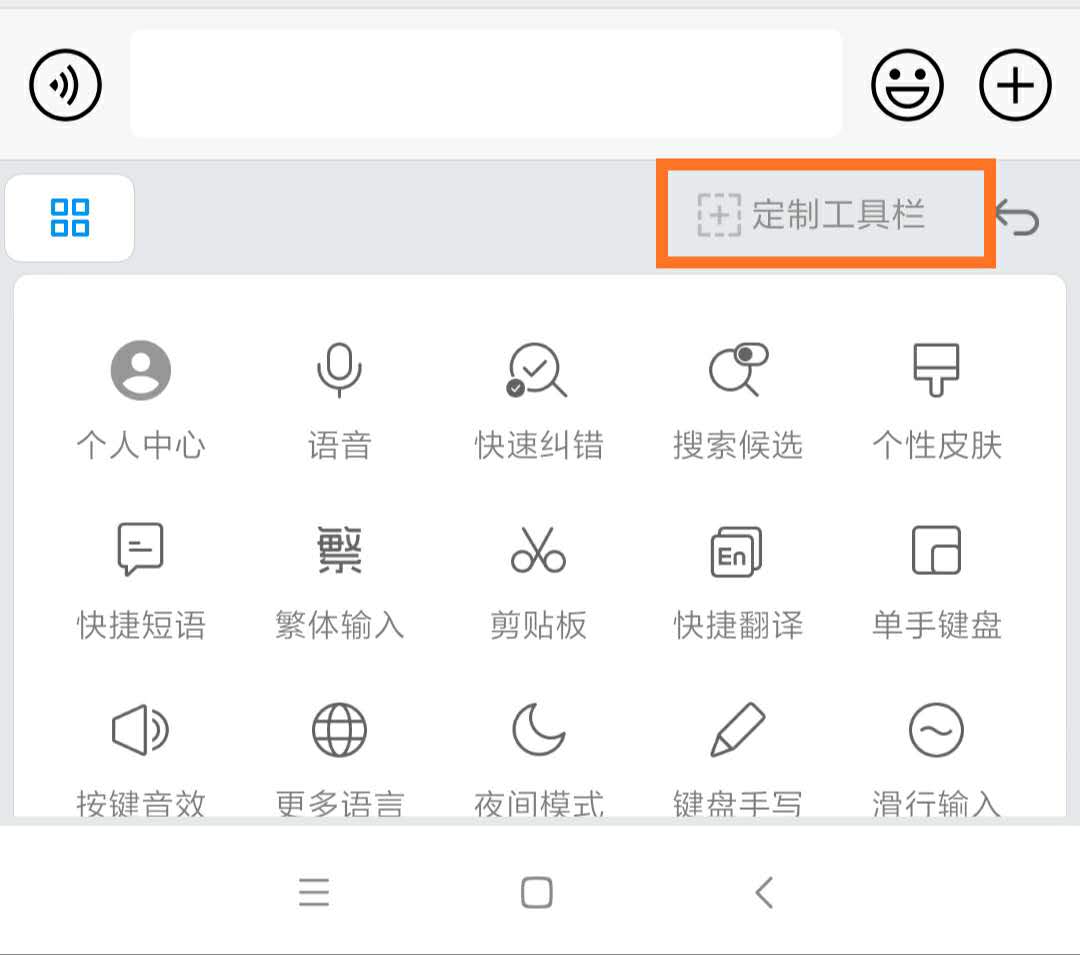
我原以为通过下图所示方法,修改工具栏选项就可以解决。

其实是不行的,这个方法只能修改这个广告左边的那些按钮。
要去掉这个广告按钮,得按如下方法操作:
设置 -> 更多设置 -> 语言和输入法 -> 搜狗输入法小米版 -> 输入习惯 -> 节日活动提醒 -> 关闭开关,搞定。
安装 udp 监测工具 netcat
1 | $ sudo yum install nc |
监听端口
1 | $ nc -vul localhost 1080 |
发送数据
1 | $ nc -vu localhost 1080 |